過去20年間、量子情報理論の中で量子計算は主に理論的な提案に留まっていました。その現実的な応用の可能性には疑問が投げかけられていましたが、最近の進展がその状況を変えつつあります。特に2019年、Googleが開発した53量子ビットの「Sycamore」量子コンピュータは、従来のコンピュータよりも遥かに高速に特定の計算を行うことができる「量子優越性」を実証しました。しかし、実用的な利用という点においてはまだまだ解決すべき問題が数多く残っています。
この新しい挑戦に応えるため、世界中の研究者たちはより有益なアルゴリズムの開発に向けて取り組んでいます。特に、量子多体理論はこの問題に対する鍵を握っています。量子物理学の舞台では、電子や原子などの目に見えない粒子が主役を演じ、これらが互いにどのように作用し合うかで、物質の性質が決まります。これらの粒子の集まりを「量子多体系」と呼び、この複雑な世界を理解することは、電子の動きから超伝導、量子コンピューターの開発に至るまで、現代科学において重要なテーマとなっています。多数の量子粒子の相互作用を扱うこの理論では、予期しない現象が起こることがあり、それを計算することの難しさを探求する研究分野がハミルトニアン複雑性です。 ハミルトニアン複雑性の研究は、量子ハミルトニアンをいつ、どのように効率的にシミュレートできるかに焦点を当てています。重要なのは、量子計算で扱う問題の多くが、QMA(量子版NP)と呼ばれるクラスに属し、これらは量子多体問題に還元できるということが知られています。つまり、量子多体問題の解決に向けたアルゴリズムの開発は、QMAクラスに属する全ての問題にアプローチするための鍵となります。 ハミルトニアン複雑性は計算機科学と物理学の間の研究領域であり、解決されていない多くの問題が数学的に定義されています。本研究室では、これらの数学的な問題に対する解決策を探求しており、量子もつれの境界則予想、量子マルコフ予想、Lieb-Robinson限界における線形光円錐問題、量子ハミルトニアン学習、有限温度における長距離量子もつれなど、重要な問題に対して部分的または完全な解決を既に達成しています。私たちの目標は、これまでの研究成果をさらに発展させ、新たな未解決問題にも取り組むことです。
当研究室メンバーらによる研究成果の一部はプレスリリースとして、一般向けに分かりやすく説明されています。
2025年10月17日
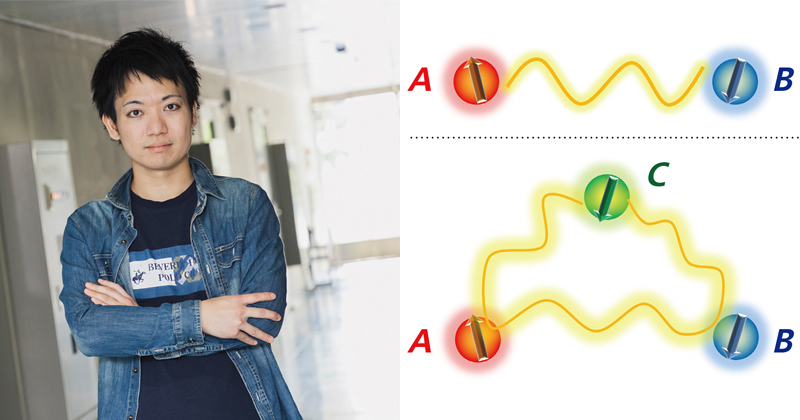
三者間量子もつれの根本的な限界を解明

2025年9月25日
量子計算による低エネルギー状態シミュレーションの大幅な効率化を達成
2025年5月13日
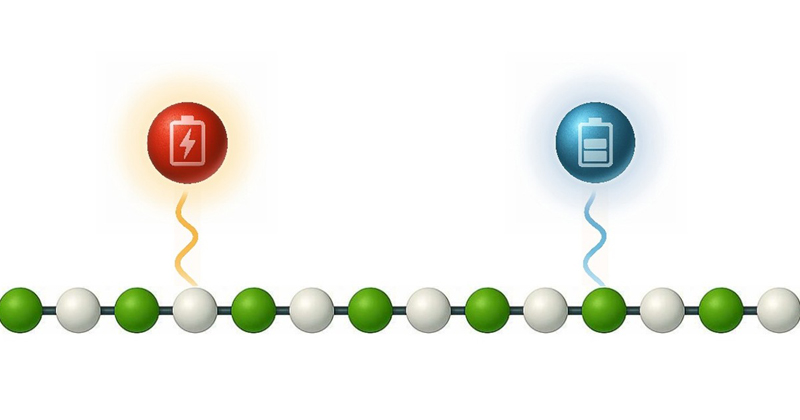
トポロジカル量子電池の理論的構築
2024年3月29日
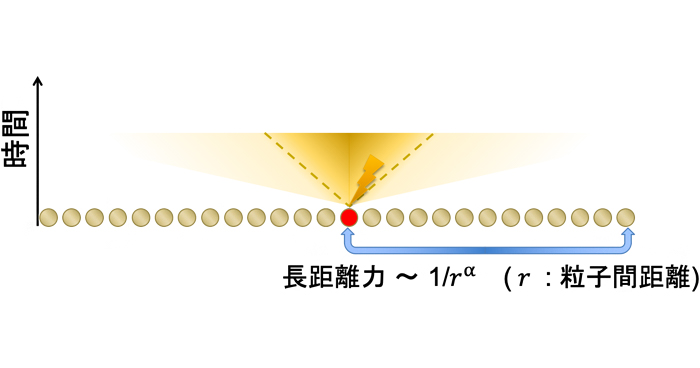
量子もつれの伝達速度限界を解明
2022年4月26日
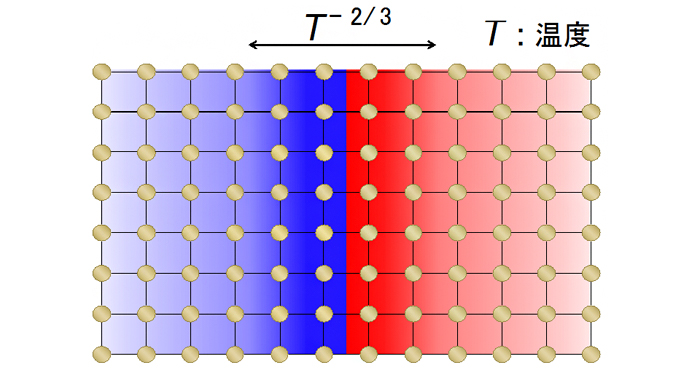
有限温度状態での量子もつれに関する普遍的性質の発見
他、理化学研究所クローズアップ科学道にも掲載されています。
「量子もつれ」における重大な性質を新発見
2022年1月6日
量子もつれに劇的な変化をもたらす新たな条件の発見
2021年5月25日
“自然界”を効率的に学習する方法を開発
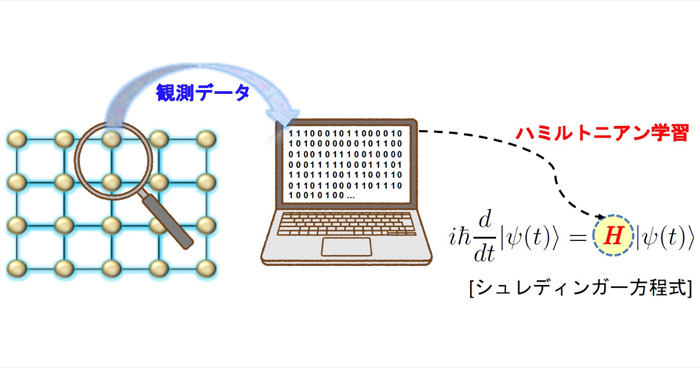
2021年3月8日
低温下における量子もつれの新法則を発見
2020年9月8日
量子もつれの境界則に対する新しいメカニズムの発見
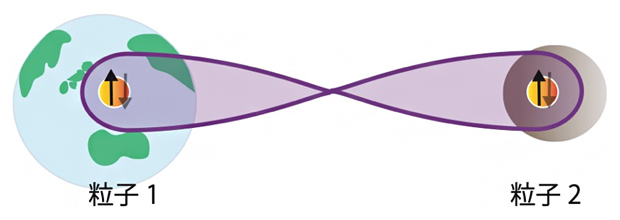
2020年7月13日
線形光円錐問題の数学的な解決